POISSON (Random) EVENTS												3
Poisson arrivals produce headways that are negative exponential distributed.
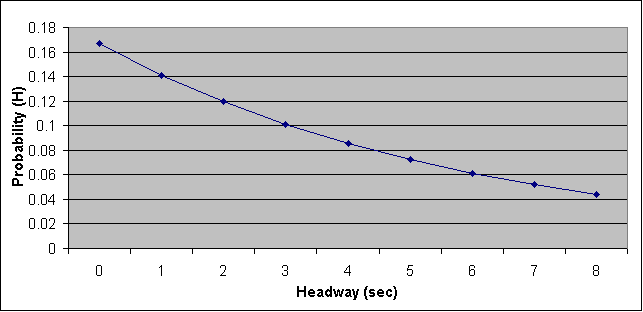
	u=	0.167
	Headway	P(H=t)
	0	0.167
	1	0.141
	2	0.119
	3	0.101
	4	0.086
	5	0.072
	6	0.061
	7	0.052
	8	0.044
IV.	P(H = t) = ue-ut
	u = lambda			Notice that short headways are more likely than long headways
What is the probability of observing a headway that is 2.5 seconds long if the mean arrival rate is 600 vph?
	u = (600 veh/hour)(1 hour/3600 sec) = 0.167 veh/hr
	P(H = 2.5)=(0.167 veh/sec)e-(0.167 veh/sec)(2.5 sec) = 0.110
V.	P(H < t) = 1-e-ut
What is the probability of observing a headway that is less than 2.5 seconds if u = 600 vph?
	P(H < 2.5)= 1 - e-(0.167 veh/sec)(2.5 sec) = 0.341
VI.	P(H >= t) = e-ut
What is the probability of observing a headway that is greater than or equal to 2.5 sec if u = 600 vph?
	P(H >= 2.5)= e-(0.167 veh/sec)(2.5 sec) = 0.659